Documentation – Current v24.2

Texture examples

Current Documentation

All documentation versions

Introduction

Part 1 of this page illustrates images analyzed in Random Scale-invariant & Dead Leaves. The images are not shown original size; they’ve been resized to be approximately equal in magnification with respect to the original chart image— with enough magnification to show the results of the camera optics and image processing.

Part 2 demonstrates how demosaicing is the cause of a commonly observed discrepancy between Spilled Coins and slanted-edge MTF measurements.

Part 1: Images used in Random / Dead Leaves

Original pattern (cropped from the middle of the chart), for reference. Original pattern (reduced from file used to print the chart)
Panasonic DMC-G3 in-camera raw, converted by dcraw with default quality setting.This image has no sharpening or noise reduction. Panasonic DMC-G3 converted from raw image by dcraw
Panasonic DMC-G3 in-camera JPEG, default settings
Typical of in-camera JPEGs, some sharpening is visible. Noise reduction is not obvious.
Panasonic DMC-G3 JPEG
Early 8 megapixel camera phoneThis image has some serious issues: poor sharpness, significant texture loss in lowest contrast areas, but it also shows sharpening-related artifacts. The left side of the image (not visible here) suffers from a serious sharpness loss.
Recent 8 megapixel camera phones (2012) have much better performance.There are some significant issues with the Spilled Coins/Dead Leaves analysis for this camera, shown in detail below. Because there seem to be a lot of artifacts around edges in the image, the Spilled Coins MTF is not bad, even though fine texture is quite absent from the image. 		 8 Megapixel camera phone
Camera phone MTF from Spilled Coins pattern (looks pretty good, but…)Here is the Spilled Coins MTF from the 8MP Camera phone. Results are pretty good, but the high frequency energy is from artifacts around edges: it is not representative of true texture detail. It would seem from this image that the Random Scale-Invariant chart might produce results that are more representative of the texture blur.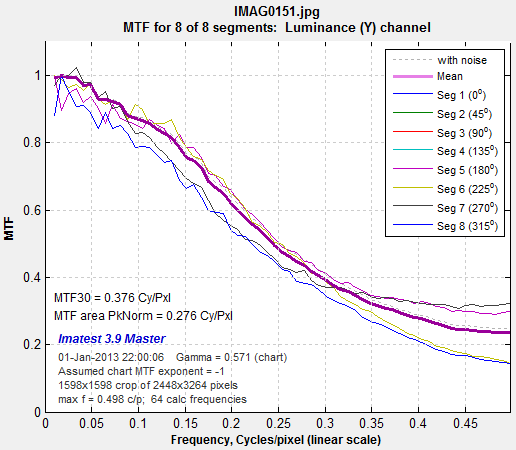
Camera phone MTF from Spilled Coins pattern
Camera phone MTF from slanted-edge. Flunnks badlyHere are the results from the slanted-edge at the bottom of the image. Results are quite poor, as expected, with little meaningful energy above 0.3 C/P. It’s a good bet that this ill-behaved camera was not included in the tests that established strong correlation from Dead Leaves-derived MTF and perceptual image quality.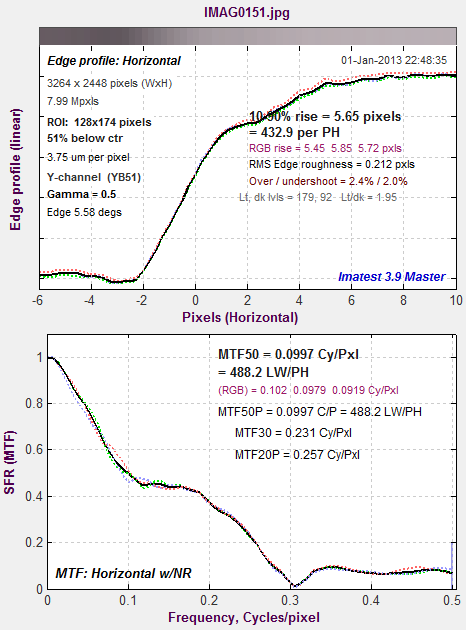
Camera phone MTF from slanted-edge.

Part 2: Spilled Coins vs. Slanted edge MTF

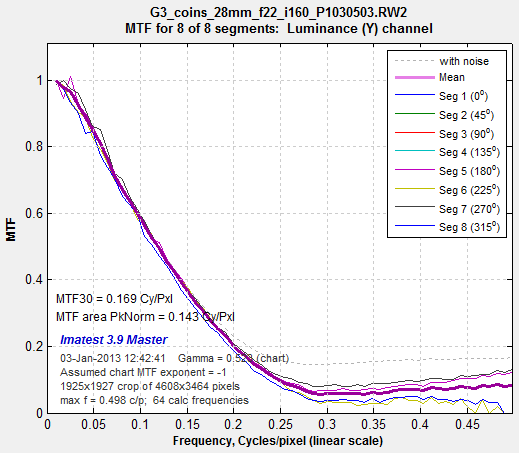
When MTF results are compared for the Spilled Coins pattern and slanted edges from the same image, we often see a discrepancy at high spatial frequencies— typically above 0.3 or 0.4 cycles/pixel, depending on the image. The Spilled Coins MTF has a floor, i.e., it doesn’t drop below a minimum value as spatial frequency increases, while the slanted-edge MTF continues to drop into the noise. We have found that this result is primarily caused by demosaicing, which involves nonlinear processing that treats edges (in the Spilled Coins pattern) differently from noise (in the smooth areas on the sides of the Spilled Coins pattern).

Summary: We have found that discrepancies between Spilled Coins and slanted-edge MTF measurements are primarily caused by demosaicing, which is a type of nonlinear processing that handles edges and random noise quite differently.

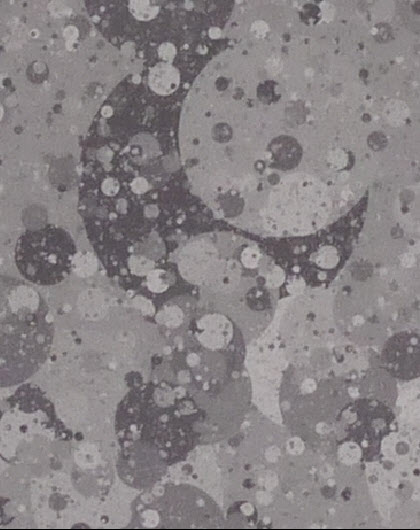
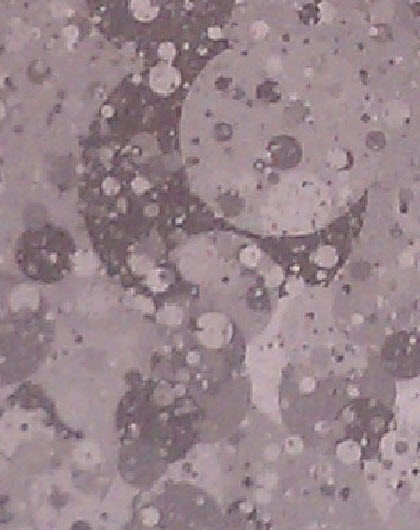
Spilled Coins MTF		 Slanted-edge MTF
Demosaiced First, we analyze a demosaiced image taken at f/22 that doesn’t have much high frequency energy. this makes it useful for looking at a single color plane of an undemosaiced image (shown below).

Spilled Coins MTF, demosaiced, f/22, ISO 160

Agreement between the two methods is excellent below 0.25 C/P, but they diverge at higher spatial frequencies. Similar results are observed at ISO 800, but curves are rougher.
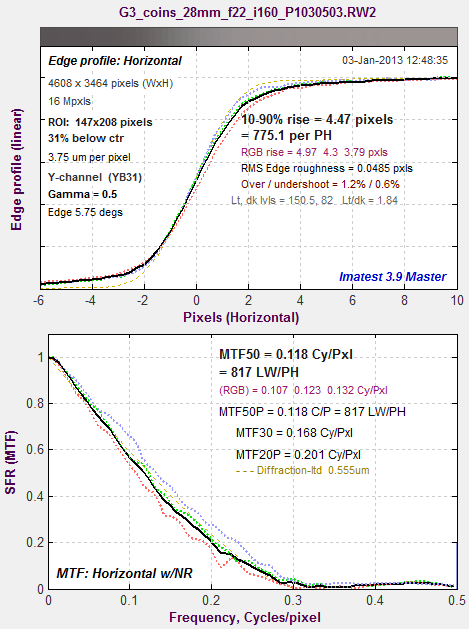Slanted-edge MTF, demosaiced, f/22, ISO 160
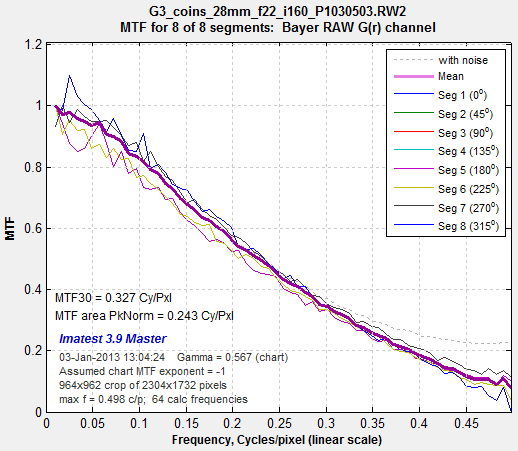
No demosaicing Next, we analyze a single color plane of the same image, undemosaiced. The number of vertical and horizontal pixels are half that of the standard demosaiced image, and the pixel pitch is double. Hence the frequencies are approximately doubled for this curve, e.g., MTF @ 0.4 C/P undemosaiced ˜ MTF @ 0.2 C/P demosaiced.

Spilled Coins MTF, demosaiced, f/22, ISO 160

Agreement between the two methods is excellent.

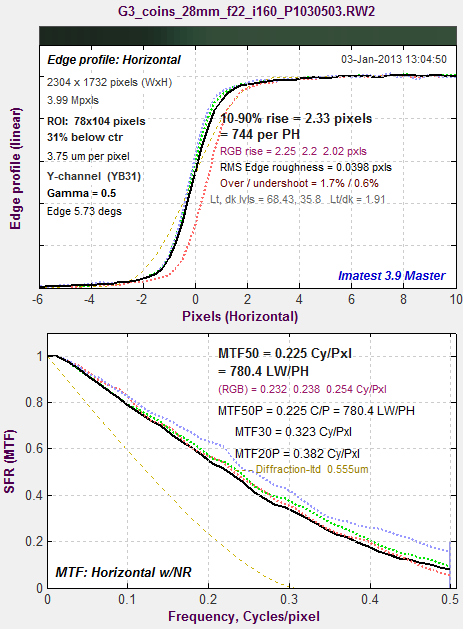 Slanted-edge MTF, undemosaiced, f/22, ISO 160
No demosaicing Finally, we analyze an image that has not been passed through a camera. It is an original image used to create the Spilled coins chart that has been reduced, linearly sharpened (USM R=2), and linearly blurred (gaussian R=1). By linear we mean perfectly uniform processing with no thresholds.

Spilled Coins MTF, original image reduced, USM sharpened (R=2), blurred (gaussian R=1)

Agreement between the Spilled Coins and slanted-edge pattern is nearly perfect.

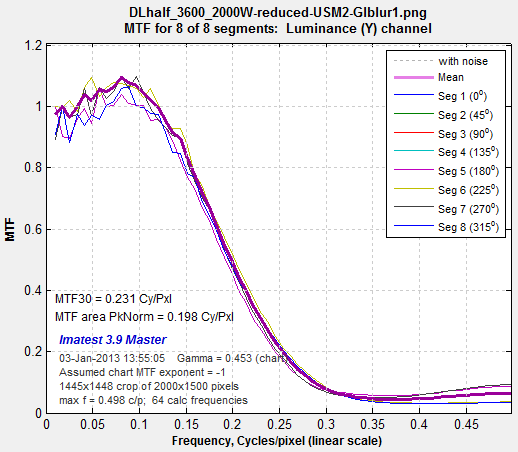
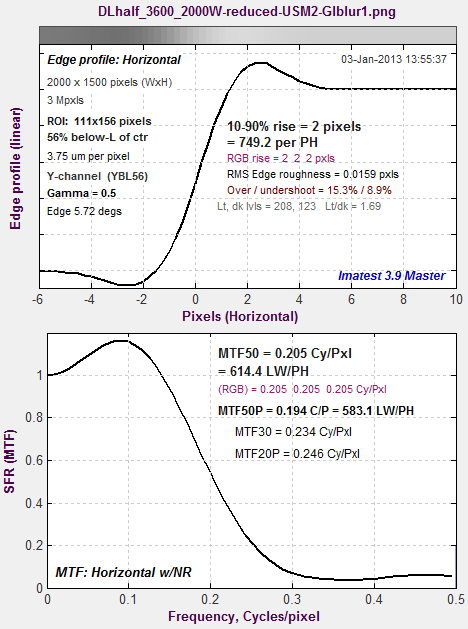Slanted-edge MTF, original image reduced, USM sharpened (R=2), blurred (gaussian R=1)